Descartes ötlete, azaz az agebrai kifejezések grafikus úton történő ábrázolása nyitotta meg az utat a dinamikusabb módszerek felé. Korábban csak statikusan létezett egy egyenlet, de ezzel a módszerrel, ha lerajzoljuk mondjuk az y=20x-5x² egyenletet, máris látjuk az egész változást. A deriválást tulajdonképpen arra használjuk, hogy megmondjuk, hogy egy görbe mennyire változik.
Ez egy rendkívül hasznos dolog. Gondoljunk csak bele, hogy milyen fontos például egy autó esetében, hogy hogyan tudja változtatni a sebességét (mekkora a gyorsulása), vagy hogy milyen egy adott értékpapír értékének a változása. A természettudományokban nagyon fontos annak a vizsgálata, hogy egy adott mennyíség milyen gyorsan változik. Ezért is nagyon fontos a deriválás.
Nézzük, hogy mi is ez a deriválásnak nevezett dolog!
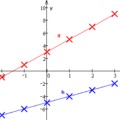
Maradjunk az y=20x-x² egyenletünknél. Tételezzük fel, hogy egy jármű sebességét ez az egyenlet írja le az idő függvényében, vagyis 0 m/s-ról indul, az első másodperc végén a sebessége 20·1-1²=19 m/s, a második másodperc végén 20·2-2²=36 m/s, stb... Az egész folyamatot az alábbi ábra szemlélteti (y tengely a sebesség, x tengely az idő másodpercben)
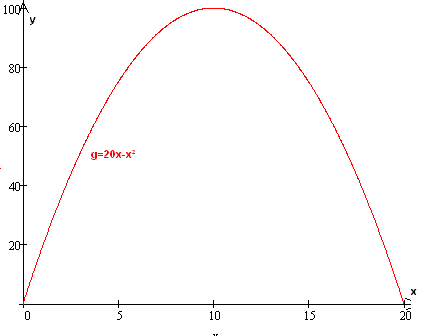 1. ábra 1. ábra |
A kérdés az, hogy mondjuk az ötödik másodpercben mennyire gyorsan változik sebesség, mekkora a gyorsulás?
Azt viszonylag egyszerűen leolvashatjuk és ki is számolhatjuk, hogy az ötödik másodpercről a hetedik másodpercre a sebesség megváltozása: y(7)-y(5)= 20·7-7²-(20·5-5²)=91-75=16 m/s. Teát két másodperc alatt 16 m/s-ot változott a sebesség. Egy másodperc alatt az átlagos sebességváltozás ezek alapján 8 m/s. Ha kiszámítjuk viszont az y(6)-y(5)-öt az y(7)-y(6)-ot, vagyis másodpercenként meghatározzuk a sebességváltozásokat, akkor azt kapjuk, hogy az ötödik és hatodik másotperc közötti sebességváltozás 9 m/s, a hatodik és hetedik közti pedig 7 m/s. Ezek így önmagukban tehán nem elég jók a sebesség változásának vizsgálatára, hiszen mindig két számhoz tartozik egy érték. Ha egyetlen ponthoz tartozna egy olyan érték, ami jellemzi a sebesség változását, az már kezelhetővé tenné a dolgokat. Erre találta ki Sir Isaac Newton, minden idők legnagyobb természettudósa a deriválást, amit anno Fluxiók módszerének nevezett.
|
|
Még mielőtt belekezdenénk Newton módszerének tárgyalásába, nézzük meg, hogy mit is csináltunk eddig geometriailag! Az ötödik másodpercről a hetedikre Δg=g(B)-g(A)=g(7)-g(5) a sebességváltozás. Az ehhez tartozó értékeket a sötötkék szaggatott vonalak jelölik a 2. ábrán. Hogy megkapjuk az átlagos sebességváltozást, a Δg-t el kell osztani a közben eltelt Δx=7-5 idővel (ezt a sötétzöld vonal jelzi). Így kapjuk meg a Δg/Δx=16/2=8 m/s²-es változást.
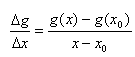 1. egyenlet 1. egyenlet |
Egyetlen pontban a sebesség változását ugyanígy tudjuk értelmezni. A lényeg, hogy Δx minnél kisebb legyen. Δx-nek azonban csak közvetetten van köze az eredeti piros g függvényünkhöz, így nem a Δx-el fogunk machinálni, hanem a függvényen lévő B pontot kezdjük el közelíteni az A ponthoz. Mivel alapjában véve B rögzített, egy általános x lesz az, ami valójában mozogni fog a függvényen. Az x neve futópont, hiszen az x nem rögzített, A-hoz közelít. Ezt a későbbiek során így fogjuk jelölni: lim(g(x))x->A, vagyis A g(x) függvény egy x pontja A-hoz tart. Ezeket a jelöléseket használva a Δg=g(x)-g(A), a Δx=A-x. Hagyományos esetben A-t x0-al szoktuk jelölni. Hogy azok számára gyorsan és egyértelműen követhető legyen a számítás, akik már találkoztak korábban is a deriválással, az A értéket mi is nevezzük el x0-nak.
Kíváncsiak vagyunk tehát a Δg/Δx=(g(x)-g(x0))/(x-x0) (1. egyenlet) értékre. Nincs is más dolgunk, mint beírni az ismert adatokat és kiszámítani az x->x0 esetet:
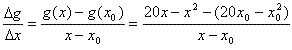 |
Első lépésként tehát helyettesítsük be a g(x)=20x-x² és a g(x0)=31x0-x0²-et! |
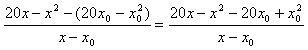 |
Bontsuk fel a zárójelet! |
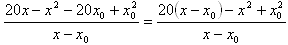 |
Emeljünk ki 20-at a 20x és a 20x0-ból! |
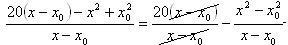 |
Válasszuk külön a számláló tagjait úgy, ahogy látjuk (figyeljünk az előjelekre!) és egyszeríthetünk x-x0-al! |
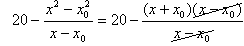 |
Az x²-x0²-et írjuk fel szorzat alakban, majd egyszerüsítsünk x-x0-al! |
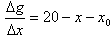 |
Ezek alapján a Δg/Δx hányados értéke 20-x-x0 |
Ha ezek után használjuk az x→x0 feltételt, vagyis hogy x végtelenül megközelíti x0-t, a kapott eredmény nem lesz más, mint 20-x0-x0, azaz a derivált értéke 20-2x0.
A fenti deriválást precízen így írjuk fel:
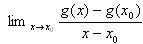 |
és azt mondjuk rá, hogy ez nem más, mind a g(x) függvény x0 pontban vett deriváltja. Ezzel a módszerrel az x0 pontban megkapjuk tehát a függvényünk gyorsulását, vagyis a függvény meredekségét.
Ha egy adott g(x) függvény minden x pontjához hozzárendelünk egy x0 pontot és ezekhez mind meghatározzuk a határértéket, akkor azzal megkapjuk g(x) deriváltfüggvényét és a következő módon jelölhetjük:
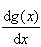 |
Analízisben gyakran alkalmazzák |
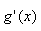 |
Tulajdonképpen egy aposztróf g felett; analízisben gyakran alkalmazzák. |
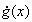 |
g pont-ként ejtik. Leggyakrabban elméleti fizikában használják és idő szerinti deriváltat jelöl, de gyakran találkozhatunk vele koordinátageometriában is. |
Fontos, hogy a három jelölés csak írásmód/megszokás kérdése. Jelentésükben nem különböznek!
A fentiek alapján a g(x)=20x-x² függvény deriváltfüggvénye a g'(x)=20-2x függvény. Ez minden pontban megadja a függvényünk érintőjéhez tartozó érintőjének a meredekségét. A g(5) gyorsulása g'(5)=20-2·5=10 m/s².

.gif) 2. ábra
2. ábra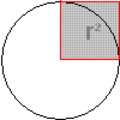

Utolsó kommentek